(solved)Question 16 SSC-CGL 2020 March 4 Shift 3

Question 16
SSC-CGL 2020 Mar 4 Shift 3

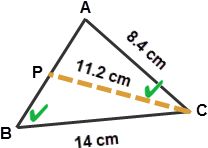
In a triangle ABC, AC = 8.4 cm, BC = 14 cm. P is a point on AB such that CP = 11.2 cm and angle ACP = angle B. What is the length BP?

Solution in Detail

Observe $\displaystyle \Delta APC$ and $\displaystyle \Delta ABC$

[1] $\displaystyle \angle ACP = \angle B \text{ [given]}$

[2] $\displaystyle \angle A \text{ [is common]}$

$\displaystyle \therefore \Delta APC \sim \Delta ABC \text{ [by AA]}$

$\displaystyle \therefore \frac{AB}{8.4} = \frac{14}{11.2} = \frac{8.4}{AP}$

From first two, $\displaystyle AB = 10.5$ cm

From last two, $\displaystyle AP = 6.72$ cm

$\displaystyle \therefore BP = AB - AP$

$\displaystyle = 10.5 - 6.72 = 3.78\text{ cm }\underline{Ans}$