(solved)Question 1 SSC-CGL 2018 June 4 Shift 1

Question 1
SSC-CGL 2018 June 4 Shift 1

In a triangle ABC, the points F and E respectively on AB and AC sides are such that FE || BC and FE divide the triangle into two parts with equal area. If AD ⊥ BC and AD intersect FE at point G, then GD: AG =?

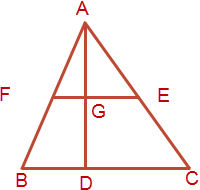
Solution in Detail

Observe in the triangles AFE and ABC

[1] $\displaystyle \angle F = \angle B$ [given FE || BC]

[2] $\displaystyle \angle E = \angle C$ [given FE || BC]

$\displaystyle \therefore $ by AA rule $\displaystyle \Delta AFE \sim \Delta ABC$

Given $\displaystyle \frac{\text{ar(ABC)}}{\text{ar(AFE)}} = 2$

$\displaystyle \therefore \bigg(\frac{AD}{AG}\bigg)^2 = \frac{\text{ar(ABC)}}{\text{ar(AFE)}} = 2$

$\displaystyle \therefore \frac{AD}{AG} = \sqrt 2$

$\displaystyle \implies \frac{(AG + GD)}{AG} = \sqrt 2$

which gives $\displaystyle \frac{GD}{AG} = (\sqrt 2 - 1) $

$\displaystyle \therefore (\sqrt 2 - 1) : 1 \:\underline{Ans}$

Solution by Alternate Method

Because of similarity,

$\displaystyle \frac{BC}{FE} = \frac{AD}{AG} = k \text{. . . (1)}$

Given, $\displaystyle\text{ ar(ABC)} = 2 \times \text{ar(AFE)}$

For a triangle, area = 1/2 x base x height

$\displaystyle \therefore \frac12 \overline{BC} \cdot \overline {AD} = 2 \cdot \frac12 \cdot \overline {FE} \times \overline{AG}$

$\displaystyle \therefore \overline{BC} \cdot \overline {AD} = 2\cdot \overline {FE} \times \overline{AG}$

Put BC and AD from (1) above

$\displaystyle \therefore k\cdot FE \cdot k\cdot AG = 2\cdot \overline {FE} \cdot \overline{AG}$

$\displaystyle \implies k = \sqrt 2$

by (1) $\displaystyle \frac{AD}{AG} = k = \sqrt 2$

$\displaystyle \implies \frac{AG + GD}{AG} = \sqrt 2$

which gives $\displaystyle \frac{GD}{AG} = (\sqrt 2 - 1) $

$\displaystyle \therefore (\sqrt 2 - 1) : 1 \:\underline{Ans}$

Solution 3

The result is independent of the type of triangle. So any triangle can be taken for verification.

Take an isosceles right angled triangle such that AF = 1 as shown.

Let $\displaystyle \overline {BF} = x$

Given, $\displaystyle\text{ ar(ABC)} = 2 \times \text{ar(AFE)}$

$\displaystyle \therefore \frac12 \cdot (1 + x) \cdot (1 + x) = 2 \cdot \frac 12 \cdot 1 \cdot 1$

Simplifying, $\displaystyle x = (\sqrt 2 - 1)$

$\displaystyle \therefore \frac{\overline{GD}}{\overline{AG}} = (\sqrt 2 - 1) : 1 \:\underline{Ans}$