Question 14
SSC-CGL 2018 June 4 Shift 1
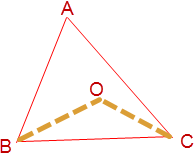
In ∆ ABC, the bisectors of ∠B and ∠C meet at point O inside the triangle. If ∠BOC = 122 degree , what will be the measure of ∠A?
- 62 degree
- 64 degree
- 72 degree
- 68 degree
Solution 1
This is a direct application of the exercises in NCERT class IX geometry. I have seen some questions being directly asked from the NCERT math books. Be clear about class VI to class XI books.A theorem has been discussed there, which states that $\displaystyle \angle \text{BOC} = 90\degree + \frac{\angle \text{A}}{2}$
we obtain, $\displaystyle \angle A = 2 \times (\angle {BOC} - 90\degree) = 64 \degree $ Ans.
Solution 2
Adding all the angles of $\displaystyle \Delta \text{OBC}$ we get $\displaystyle \angle \text{BOC} + \frac{\angle \text{B}}{2} + \frac{\angle \text{C}}{2} = 180 \degree$
$\displaystyle \implies 122 \degree + \frac{\angle \text{B}}{2} + \frac{\angle \text{C}}{2} = 180 \degree$
$\displaystyle \implies \angle \text{B} + \angle \text{C} = 116\degree$
By the sum of angles of $\displaystyle \Delta \text{ABC}$ we get $\displaystyle \angle \text{A} = 180\degree - (\angle \text{B} + \angle \text{C}) = 64 \degree$ Ans.
EXPLANATION: A triangle ABC has been given whose angle A is to be found out. But we have been given that the angle bisectors of angle B and C meet somewhere inside the triangle at a point O forming an angle BOC of 122 degree. In every book on elementary geometry, there is a relation between the angle A and the angle BOC. With the angle of BOC as 122, the value of angle A is fairly easy to calculate.
Solution 3
Use the fact that the sum of interior angles of a quadrilateral is $\displaystyle 360 \degree$
From the quadrilateral ABOC, $\displaystyle \angle A + \frac{\angle B}{2}+ \frac{\angle C}{2} + (360\degree - 122\degree)$ = $\displaystyle 360 \degree$
$\displaystyle \implies \angle A + \frac{\angle B}{2}+ \frac{\angle C}{2} = 122 \degree$
$\displaystyle \implies \frac{\angle A}{2} + \bigg(\frac{\angle A}{2} + \frac{\angle B}{2}+ \frac{\angle C}{2}\bigg) = 122 \degree \text{*}$
$\displaystyle \implies \frac{\angle A}{2} + 90 \degree = 122 \degree$
$\displaystyle \implies \angle A = 64 \degree$ Ans!
*EXPLANATION: We have split $\displaystyle \angle A $ as $\displaystyle \frac{\angle A}{2} + \frac{\angle A}{2}$

This Blog Post/Article "(solved)Question 14 SSC-CGL 2018 June 4 Shift 1" by Parveen is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.