(solved)Question 1 SSC-CGL 2020 March 3 Shift 1

Question 1
SSC-CGL 2020 Mar 3 Shift 1

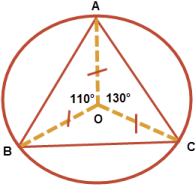
Chords AB and AC subtend angles of 110° and 130° at the center of a circle as shown. The angle BAC = ?

Solution in Brief

Let O be the center of the circle. Angle BOC = 360° - (110° + 130°) = 120°, which gives the angle on the arc as BAC = 120°/2 = 60° answer!

Solution in Detail

Adding angles at the center,

$\displaystyle \angle{\text{BOC}}$ + $\displaystyle 110\degree$ + $\displaystyle 130\degree$ = $\displaystyle 360\degree$

$\displaystyle \implies \angle{\text{BOC}} = 120 \degree$

$\displaystyle \implies $ subtended $\displaystyle \angle {\text{BAC}} = \frac{\angle{\text{BOC}}}{2}$

$\displaystyle \implies \angle {\text{BAC}} = 60\degree \:\underline{Ans}$