(solved)Question 2 SSC-CGL 2020 March 4 Shift 3

Question 2
SSC-CGL 2020 Mar 4 Shift 3

A sold an article to B at a loss of 20%. B sold it to C at a profit of 12.5%. C sold it to D at a loss of 8%. D pays Rs 248.4 for that article. Find the difference of loss incurred by A and C.

Solution in Short

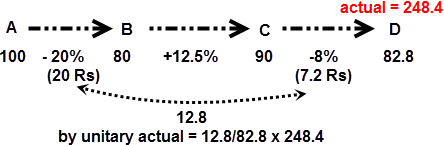
Take CP of A = 100. His loss is 20. Hence the CP of B is 100 - 20 = 80. B sells to C at 80 + 12.5% = 90. But C sells further to D at a loss of 8%, i.e, of 8/100 x 90 = Rs. 7.2. The cost to D is 90 - 7.2 = 82.8. Next use unitary method: If cost to D is 82.8, the difference of losses of C and A is 20 - 7.2 = 12.8. But if cost to D is 248.4, the difference would be 12.8/82.8 x 248.4 = 38.4 ans!

Solution in Detail

Let CP of A = $\displaystyle 100$

A sells at 20% loss

[1] $\displaystyle \therefore $ loss of A = $\displaystyle 20\% = 20$

SP of A is $\displaystyle 100 - 20 = 80$

SP of A is CP of B

$\displaystyle \therefore $ CP of B is $\displaystyle 80$

B sells to C at 12.5% profit.

SP of B $\displaystyle = 80 + 12.5\% = 90$

C sells to D at 8% loss.

[2] Loss of C = $\displaystyle 8\% \text{ of } 90 = 7.2$

SP of C $\displaystyle = 90 - 7.2 = 82.8$

SP of C becomes CP of D

$\displaystyle \therefore $CP of D $\displaystyle = 82.8$

Diff. of losses of C and A is [2] - [1]

$\displaystyle = 20 - 7.2 = 12.8$

Now set the unitary method:

If CP of D is $\displaystyle 82.8$, then diff = $\displaystyle 12.8$

But CP of D given = 248.4 Rs. Therefore, if CP of D is $\displaystyle 248.4$ then the difference of losses of C and A

$\displaystyle = \frac{12.8}{82.8} \times 248.4 = 38.4\:\underline{Ans}$