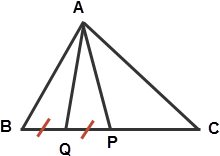
(solved)Question 1 SSC-CGL 2019 June 13 Shift 1 | In ΔABC, P is a point on BC such that BP : PC = 4 : 11. If Q is the midpoint of BP, then ar(ΔABQ) : ar(ΔABC) is equal to?

Parveen, Mar 01, 2020

In ΔABC, P is a point on BC such that BP : PC = 4 : 11. If Q is the midpoint of BP, then ar(ΔABQ) : ar(ΔABC) is equal to?

We have been given BP = 4k, which gives BQ = 2k. We have also been given PC = 11k, so BC = BP + PC = 15k.

If heights of triangles are same, then the ratio of their areas is same as the ratio of their bases.

Base of ΔABQ is BC = 15k, and of ΔABQ is BQ = 2k, and therefore, the ratio of their areas is 2k : 15k which is same as 2 : 15 answer!

Given BP = 4k and PC = 11k

$\displaystyle \therefore $ base of ΔABC is BC = BP + PC = 15k

and of triangle ABQ is BQ = $\displaystyle \frac{\text{BP}}{2} = 2k$.

Now, area of any triangle is $\displaystyle \frac 12 \times \text{b} \times \text{h}$

[1] $\displaystyle \therefore$ ar(ΔABC) $\displaystyle = \frac12 (15\text{k})(\text{h}) = 15\text{kh}/2$

[2] and ar(ΔABQ) $\displaystyle = \frac12 (2\text{k})\text{h} = \text{kh}$

$\displaystyle \therefore \frac{\text{ar(ABQ)}}{\text{ar(ABC)}} = \frac{\text{hk}}{(15\text{hk}/2)}$

= 2 : 15 answer!

This Blog Post/Article "(solved)Question 1 SSC-CGL 2019 June 13 Shift 1" by Parveen is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.