(solved)Question 12 SSC-CGL 2018 June 4 Shift 1

Question 12
SSC-CGL 2018 June 4 Shift 1

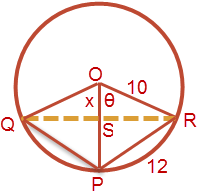
The radius of a circle with O center is 10 cm, PQ and PR are the chords of 12 cm. PO cuts the chord QR at point S. What is the length of OS?

1. 3.2 cm
2. 2.8 cm
3. 3 cm
4. 2.5 cm

Solution 1

Apply cosine formula to the isosceles $\displaystyle \Delta OPR$.

$\displaystyle 12^2 = 10^2 + 10^2 - 2\cdot 10 \cdot 10 \cos \theta$

$\displaystyle \implies \cos \theta = 0.28$

From the right triangle (why? chord bisector theorem) $\displaystyle \Delta OSR$, $\displaystyle x = 10 \cos \theta = 10 \times 0.28 = $ 2.8 cm Ans!

EXPLANATION: the circle has a radius of 10 cm. Two of its chords PQ and PR are co-terminus at P. The lengths of the two chords are each equal to 12 cm. The points P, Q, R, S and the center O of the circle form a quadrilateral. The diagonals PO and QR intersect at S. Observe that OP is a radius of the circle that is intersecting the chord QR. The angle of intersection will be 90 degree because each radius of a circle is the perpendicular bisector of each chord of the circle. Once, we establish that OS is perpendicular to QR, we are in a position to apply pythagoras theorem and other trigonometric formulae.

Solution 2

By pythagoras to triangle OSR, $\displaystyle \overline{SR}^2 = 10^2 - x^2\text{ . . . (1)}$

By pythagoras to triangle PSR, $\displaystyle \overline{SR}^2 = 12^2 - (10 - x)^2\text{ . . . (2)}$

Equating and simplifying, we can get x = 2.8 cm Ans!

This Blog Post/Article "(solved)Question 12 SSC-CGL 2018 June 4 Shift 1" by Parveen is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.