(solved)Question 9 SSC-CGL 2018 June 4 Shift 2 | A circle inside a triangle ABC, whose center O is created. On increasing AO, it meets the circle [or triangle] on K and AD ⊥BC. If ∠B = 80° and ∠C = 64°, then the measure of ∠DAK is?

Parveen, Feb 20, 2020

Question 9
SSC-CGL 2018 June 4 Shift 2

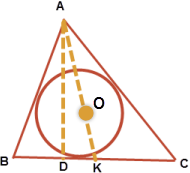
A circle inside a triangle ABC, whose center O is created. On increasing AO, it meets the circle [or triangle] on K and AD ⊥BC. If ∠B = 80° and ∠C = 64°, then the measure of ∠DAK is?

10°
12°
20°
8°

Solution 1

Sum of the angles of a triangle is $\displaystyle 180 \degree$, so from the given values of B and C we calculate $\displaystyle \angle A = 36\degree$

The angle bisectors of a triangle meet at a common point called in-center, which is the center of the circle that can be inscribed in the triangle.

Hence, AK is the bisector of angle A, which gives $\displaystyle \angle BAK = 18\degree$

To obtain $\displaystyle \angle DAK$, we have to know the value of $\displaystyle \angle BAD$

The triangle $\displaystyle \Delta ABD$ is right angled, out of which $\displaystyle \angle B$ has been given as $\displaystyle 80 \degree,$ so we conclude $\displaystyle \angle {BAD} = 10\degree$

$ \begin{aligned} \implies \angle DAK &= \angle BAK - \angle BAD\\ &= 18 - 10 = 8 \degree \:\underline{Ans} \end{aligned} $

Solution 2

$\displaystyle \Delta \text{ADC}$ is a right angled triangle, with $\displaystyle \angle C$ already given as $\displaystyle 64\degree, $ so that $\displaystyle \angle DAC = 90 - 64 = 26\degree$

But AK is the angle bisector of angle A as explained in method 1. So, $\displaystyle \angle KAC = 18\degree$

Finally, $\displaystyle \angle DAK = \angle DAC - \angle KAC$ = 26 - 18 = $\displaystyle 8\degree$ answer!

Solution 3

AK is the bisector of angle A so $\displaystyle \angle {BAK}$ = $\displaystyle 18 \degree$ as already explained above.

By exterior angle theorem applied to triangle ABK, we conclude

$\displaystyle \angle {AKC}$ = $\displaystyle \angle B$ + $\displaystyle \angle BAK$ = $\displaystyle 80 + 18$ = $\displaystyle 98\degree$

Again apply exterior angle theorem to $\displaystyle \Delta DAK$, to get

$ \begin{aligned} \angle DAK + \angle D &= \angle {AKC}\\ \therefore \angle DAK + 90\degree &= 98\degree\\ \implies \angle DAK &= 8\degree\:\underline{Ans} \end{aligned} $