(solved)Question 11 SSC-CGL 2018 June 4 Shift 2

Question 11
SSC-CGL 2018 June 4 Shift 2

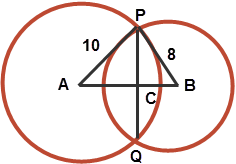
Circles of radius 10 cm and 8 cm cut each other at points P and Q. PQ = 12 cm and the distance between the centers of the circle is x cm, then the value of x (correct to 1 decimal place):

1. 14.8
2. 12.8
3. 13.9
4. 13.3

Solution in Short

PQ of 12 cm is bisected at C giving PC = 6 cm. APC is a right triangle with AP = 10 cm and PC = 6 cm. But 6, 8 and 10 are pythagorean triplets, so AC = 8 cm.

Likewise, triangle PCB is right angled with PB = 8 cm and PC = 6 cm. By pythogaras theorem, CB² = 28, which gives CB = 2 x sqrt 7 ≈ 5.3 cm.

Finally, AB = AC + CB = 13.3 cm answer!

Solution in Detail

$\displaystyle \implies \overline {\text{PC}} = \frac{\overline{\text{PQ}}}{2} = 6$ cm.

[1] The right $\displaystyle \Delta {APC}$ has sides 10 and 6.

But 10, 6 and 8 are pythagorus triplets.

$\displaystyle \therefore $ third side $\displaystyle \overline{\text{AC}} = 8 \text{ cm. . . (1)}$

[2] $\displaystyle \Delta {PCB}$ is also right angled.

$ \begin{aligned} \therefore \overline{\text{CB}} &= \sqrt{8^2 - 6^2}\\ &=\sqrt{28}\\ &= \sqrt{4 \times 7}\\ &= 2 \sqrt{ 7}\\ &= 2 \times 2.65 \\ &= 5.3 \text{ cm. . . (2)}\\ \end{aligned} $

Adding $\displaystyle \text{(1)}$ and $\displaystyle \text{(2), } 13.3 \text{cm }\:\underline{Ans}$

This Blog Post/Article "(solved)Question 11 SSC-CGL 2018 June 4 Shift 2" by Parveen is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.