(solved)Question 11 SSC-CGL 2020 March 3 Shift 1

Question 11
SSC-CGL 2020 Mar 3 Shift 1

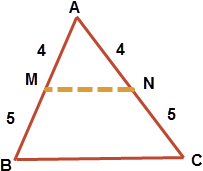
In a triangle ABC, M and N are points on AB and AC respectively, such that MN is parallel to BC and AN : NC is 4 : 5. If the area of the quadrilateral MNCB is 130 sq. units, then what is the area of triangle MAN?

Solution in Brief

Triangles ABC and AMN are similar with ratio of sides as 9/4. So area ABC = 81/16 x area AMN. But area ABC = area AMN + 130. So area AMN + 130 = 81/16 x area AMN. Solving, area AMN = 32 sq. units ans!

Video Explanation (slow explanation)

Please watch this slow and easy explanation:

Solution in Detail

Observe the triangles AMN and ABC

[1] Given that MN ∥ BC, so $\displaystyle \angle M = \angle B$

[2] Given that MN ∥ BC, so $\displaystyle \angle N = \angle C$

$\displaystyle \therefore$ by AA rule, $\displaystyle \Delta ABC \sim \Delta AMN$

Ratio of similar sides $\displaystyle \frac{4k + 5k}{4k} = \frac 94$

$\displaystyle \therefore \frac{\text{ar(ABC)}}{\text{ar(AMN)}} = \bigg(\frac 94\bigg)^2$

$\displaystyle \therefore \text{ar(ABC)} = \frac{81}{16} \times \text{ar(AMN)}$

But triangle ABC is sum of triangle AMN and the quadrilateral MNCB whose area given as 130

For simplicity let, $\displaystyle x = \text{ar(AMN)}$

$\displaystyle \therefore 130 + x = \frac{81}{16} \times x$

Solving, $\displaystyle x = \text{ar(AMN)} = 32\:\underline{Ans}$