Question 6
SSC-CGL 2020 Mar 4 Shift 2
In a circle, AB and CD are two chords. When they are extended, they meet at a point P outside the circle such that AB = 7cm, BP = 4.2cm and DP = 2.8cm. Find the length of chord CD?
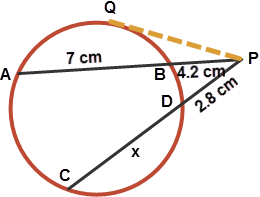
Solution in Detail
Remember: Secant-Tangent theorem states that if a chord AB is extended to point P outside the circle, and PQ is a tangent, then PQ² = AP x BPby secant tangent theorem for APQ
$\displaystyle PQ^2 = AP \times BP$
$\displaystyle \text{i.e., } = (7 + 4.2) \times 4.2$
$\displaystyle \therefore PQ^2 = 11.2 \times 4.2\text{. . . (1)}$
Similarly, for CPQ,
$\displaystyle PQ^2 = (2.8 + x) \times 2.8\text{. . . (2)}$
Equating (1) and (2)
$\displaystyle (2.8 + x) \times 2.8 = 11.2 \times 4.2$
Solving, $\displaystyle x = 14\text{ cm }\underline{Ans}$

This Blog Post/Article "(solved)Question 6 SSC-CGL 2020 March 4 Shift 2" by Parveen is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.