(solved)Question 10 SSC-CGL 2020 March 4 Shift 3

Question 10
SSC-CGL 2020 Mar 4 Shift 3

How many numbers are there between 200 and 800 that are neither divisible by 5 nor by 7?

Solution in Short

Total numbers between 200 to 800 are 599. Out of them divisible by 5 are 119 [see detailed explanation below], and by 7 are 86. So count of numbers divisible by 5 or 7 are 119 + 86 = 205. But this includes those that are divisible both by 5 and 7, and have been counted in both the lists. Such numbers are those that are divisible by 5 x7 = 35, whose count is 16. So numbers that are divisible by 5 or 7 are 205 - 17 = 188. The required remaining that are divisible by none are 599 - 189 = 411 ans!

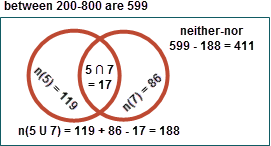
Solution in Detail

First count how many divisble by 5

Observe 200 = 5 x 40, 800 = 5 x 160

$\displaystyle \therefore n(5) = 160 - 40 - 1 = 119$

[Excluded 200 and 800]

Also, 203 = 7 x 29, 798 = 7 x 114

$\displaystyle \therefore n(7) = 114 - 29 + 1 = 86$

[included both 203 and 798]

But how many by both 5 and 7?

So we count those that are divisible by 5 x 7 = 35. It will give those that are divisible by both 5 and 7.

Observe 210 = 35 x 6, 770 = 35 x 22

$\displaystyle \therefore n(5 \cap 7) = 22 - 6 + 1 = 17$

Divisible by 7 or 5 [revise your Venn]

$\displaystyle = n(5) + n(7) - n(5\cap 7)$

$\displaystyle = 119 + 86 - 17 = 188$

Total between 200 to 800 are 599

Remaining $\displaystyle = 599 - 188 $

$\displaystyle = 411\:\underline{Ans}$