(solved)Question 8 SSC-CGL 2020 March 4 Shift 3

Question 8
SSC-CGL 2020 Mar 4 Shift 3

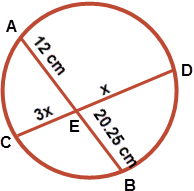
Chords AB and CD of a circle intersect at E. If AE = 12cm, BE = 20.25cm and CE = 3DE. Find the length of CE?

Solution in Brief

Two intersecting chords have a property that CE x ED = AE x EB. Putting the given values 3x × x = 12 × 20.25. Which gives x² = 81, or x = 9 ans!

Solution in Detail

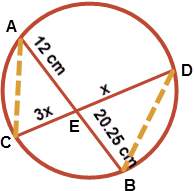
Observe $\displaystyle \Delta CAE$ and $\displaystyle \Delta EDB$

Vertically opposite angles at E

[1] $\displaystyle \angle CEA = \angle BED$

Angles on the same chord CB

[2] $\displaystyle \angle CAB = \angle CDB$

By AA rule $\displaystyle \Delta CAE \sim \Delta EDB$

$\displaystyle \therefore \frac{CE}{EB} = \frac{AE}{ED}$

$\displaystyle \therefore \frac{3x}{20.25} = \frac{12}{x}$

whence, $\displaystyle x = 9\:\underline{Ans}$