(solved)Question 4 SSC-CGL 2019 June 13 Shift 1

Question 4
SSC-CGL 2019 June 13 Shift 1

In a class of 50 students, 40% are girls. The average marks of the whole class are 64.4 and the average of the boys' marks is 62. What is the average marks of the girls?

1. 67
2. 66.8
3. 66.4
4. 68

Solution in Short

Required average = A. Weighted average is 62 x 0.6 + A x 0.4 = 64.4, which can be simplified to obtain A = 68 answer!

Solution in Detail

Girls in the class are $\displaystyle 40\% \text{ of } 50 = 20$

$\displaystyle \therefore $ boys are $\displaystyle 50 - 20 = 30$

[1] Average score of boys given as $\displaystyle 62$

$\displaystyle \therefore $ total score of boys $\displaystyle 62 \times 30 = 1860$

[2] Average of whole class given as $\displaystyle 64.4$

$\displaystyle \therefore $ total of whole class $\displaystyle 64.4 \times 50 = 3220$

$\displaystyle \therefore$ total of girls = $\displaystyle 3220 - 1860 = 1360$

$\displaystyle \therefore $ average of girls $\displaystyle = \frac{1360}{20} = 68$ ans!

Solution by Mixtures

Class is a mixture (boys + girls)

[1] Average of boys is 62, and of girls is x

[2] Ratio of boys to girls is $\displaystyle \frac{60\%}{40\%} = \frac {60}{40}$

[3] Average of mixture = 64.4 (given)

Draw the diagram as below

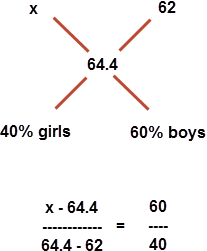
On calculation, x = 68 answer!