(solved)Question 11 SSC-CGL 2020 March 3 Shift 2

A circle is inscribed in a quadrilateral as shown. If AB = 7 cm, BC = 6 cm and CD = 8 cm, then the length of AD is?
(Rev. 31-Oct-2024)

Categories | About Hoven's Blog

Parveen,

Question 11
SSC-CGL 2020 Mar 3 Shift 2

A circle is inscribed in a quadrilateral as shown. If AB = 7 cm, BC = 6 cm and CD = 8 cm, then the length of AD is?

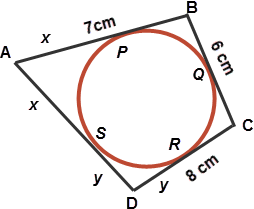
Solution in Brief

By geometry, AB + DC = AD + BC, which gives AD = 9 cm ans!

Solution in Detail

Remember: Tangents to a circle from an external point are equal

Let $\displaystyle AS = x, SD = y$

[1] $\displaystyle BQ = BP = 7 - x$

[2] $\displaystyle QC = CR = 8 - y$

But $\displaystyle BQ + QC = 6$

$\displaystyle \therefore (7 - x) + (8 - y) = 6$

$\displaystyle \implies x + y = 9$

$\displaystyle \therefore AD = x + y = 9\:\underline{Ans}$

Creative Commons License
This Blog Post/Article "(solved)Question 11 SSC-CGL 2020 March 3 Shift 2" by Parveen is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.