(solved)Question 2 SSC-CGL 2020 March 4 Shift 1

Question 2
SSC-CGL 2020 Mar 4 Shift 1

ABCD is a cyclic quadrilateral in which AB = 16.5 cm, AD = 11 cm and CD = 19.8 cm. If AC bisects BD, then what is the measure of BC?

Solution in Brief

If a diagonal of the cyclic quadrilateral is bisected, then the products of adjacent sides touching it is equal. Why is it so? For this see the "Solution in Detail" below.

$\displaystyle AB \cdot BC = AD \cdot DC$

$\displaystyle \therefore 16.5 \times x = 19.8 \times 11$

$\displaystyle \therefore x = 13.2 \text{ cm }\underline{Ans}$

Solution in Detail

Consider a cyclic quadrilateral ABCD whose diagonals intersect at P as shown in the figure below

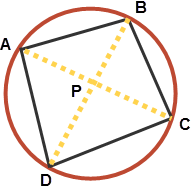
Then it can be proved that

$\displaystyle \frac{PB}{PD} = \frac{AB}{AD} \cdot \frac{BC}{DC}$

But if BD is bisected at P, so PB = PD

$\displaystyle \therefore1 = \frac{AB}{AD} \cdot \frac{BC}{DC}$

Then we can proceed as above.