(solved)Question 9 SSC-CGL 2020 March 4 Shift 1

Question 9
SSC-CGL 2020 Mar 4 Shift 1

In a right-triangle ABC, angle A = 90 degree, AB = 7cm, AC = 24cm. M is the mid-point of BC and AD⊥BC. Find AM : AD?

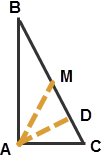
Solution in Detail

ABC is a right triangle with two sides AC = 24 and AB = 7 cm. But 24, 25 and 7 are a pythagorean triplets.

$\displaystyle \therefore \text{third side } BC = 25$ cm

Given M is midpoint of BC

$\displaystyle \therefore BM = \frac{BC}{2} = 12.5$ cm

By properties of right triangle,

[1] $\displaystyle AM = BM = \frac{25}{2} \text{ cm}$

Again, given AD⊥BC

By properties of right triangle,

$\displaystyle BC \cdot AD = AC \cdot AB$

$\displaystyle \therefore AD = \frac{AC \cdot AB}{BC}$

[2] $\displaystyle \therefore AD = \frac{24 \times 7}{25}$

Divide by [1] and [2], the ratio

AM : AD $\displaystyle = \frac{25 \times 25 }{2 \times 24 \times 7}$

$\displaystyle = \frac{625}{336}\:\underline{Ans}$

Additional Discussion of Why AM = BM?

A is a right angle, and an angle in a semi-circle is a right angle. So BC can be a diameter of a circle that passes through B, A and C.

Obviously, AM is a radius, i.e, half of the diameter BC. Hence AM = BM!

Additional Discussion of Why AD x BC = AB x AC?

Area of the right triangle ABC with base AC is = 1/2 x AB x AC

Again, the area of the same triangle viewing with base BC is 1/2 x AD x BC

Equating both the values of the area we get the result AD x BC = AB x AC!