(solved)Question 11 SSC-CGL 2020 March 4 Shift 1 | In a triangle ABC, AB = AC. A circle is drawn from vertex B such that it touches the side AC at D (where D is the mid-point of AC) and it cuts the side AB at E where AE = 2.5cm. Find the length of side AB.

Parveen, Mar 11, 2020

Question 11
SSC-CGL 2020 Mar 4 Shift 1

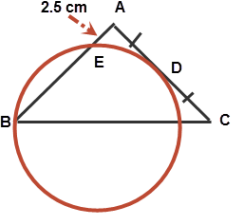
In a triangle ABC, AB = AC. A circle is drawn from vertex B such that it touches the side AC at D (where D is the mid-point of AC) and it cuts the side AB at E where AE = 2.5cm. Find the length of side AB.

Solution in Detail

This question is based on the tangent secant theorem of elementary geometry, also discussed in NCERT class IX Math book. Or, you can refer wikipedia for the tangent secant theorem

Given D is midpoint of AC

$\displaystyle \therefore AD = \frac{AC}{2}$

But also given AC = AB

$\displaystyle \therefore AD = \frac{AB}{2}\text{. . . (1)}$

Observe that AD is a tangent and AEB is a secant. So the tangent secant theorem can be applied:

$\displaystyle AD^2 = AE \times AB$

Using (1), and also that AE = 2.5 cm,

$\displaystyle \bigg(\frac{AB}{2}\bigg)^2 = 2.5 \times AB$

$\displaystyle \implies AB = 10 \text{ cm }\underline{Ans}$