(solved)Question 12 SSC-CGL 2020 March 4 Shift 3

Question 12
SSC-CGL 2020 Mar 4 Shift 3

Two circles of radius 5 cm and 7 cm intersect at two points A and B. if the distance between the centres of two circles is 10 cm, then find the length of the common chord.

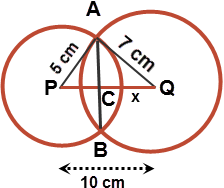
Solution in Brief

In triangle APQ, the sides are 5, 7 and 10 cm. Using heron's formula we can find its area. s = semi-perimeter = (5 + 7 + 10)/2 = 11, so A = √ (s(s-a)(s-b)(s-c)) = √(11 x 6 x 4 x 1) = 2√66. Area of the triangle is also 1/2 x base x height = 1/2 x PQ x AC = 1/2 x 10 x AC. Equating the two areas, AC = 2√66/5. So AB = 2 x AC = 4√66/5 answer!

Solution in Detail

We have $\displaystyle PQ \perp AC$

$\displaystyle \therefore \Delta ACQ$ is right angled

[1] $\displaystyle \therefore AC^2 = 7^2 - x^2$

Likewise from $\displaystyle \Delta ACP$

[2] $\displaystyle \therefore AC^2 = 5^2 - (10 - x)^2$

by [1] and [2] on simplification

$\displaystyle x = \frac{31}{5}$

$\displaystyle \therefore AC^2 = 7^2 - \bigg(\frac{31}{5}\bigg)^2$

$\displaystyle \therefore = \bigg(7^2 - \frac{31^2}{5^2}\bigg)$

$\displaystyle = \bigg(\frac{35^2 - 31^2}{5^2}\bigg)$

$\displaystyle = \frac{(35 - 31)(35 + 31)}{5^2}$

$\displaystyle =\frac{4 \times {66}}{5^2}$

$\displaystyle \therefore AC = \sqrt{\frac{4 \times 66}{5^2}} = \frac{2\sqrt {66}}{5}$

Finally, $\displaystyle AB = 2\cdot AC$

$\displaystyle = \frac{4\sqrt {66}}{5}\:\underline{Ans}$